Logo Demos

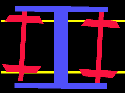Logo Motion of a bogie

The bogie of a railroad car is a multibody system connected with springs and dampers. The parts (basically wheels, axis, and frame) respond to outer impact. The motion of the multibody system obeys a dynamical law, and can be calculated by means of numerical methods. The quality of the response essentialy depends on the speed v of the bogie. The program (written in FORTRAN) calculates and plots the dynamics. The speed v can be chosen freely.

Download plain Vga-PC Executable

Response to an initial pertubation, depending on the speed v [km/h].

Logo v=220 : stationary motion survives (1,1 MB mpeg)

Logo v=260 : periodic motion takes over (1,2 MB mpeg)

Logo v=650 : somewhat irregular (1,5 MB mpeg)

See also example exd10 and hassard's worksheet.

LogoDancing balls

A ball under gravity is attracted by the minima of the surrounding landscape. Here we have a valley with a hillock in the middle. Clearly the top of the hillock is a repellot for the ball. Depending on the initial state (coordinate x and velocity v) the ball choose a trajectory towards one of the two stable attractors / minima. Close initial states may end up in different attractors! (Example: compare x=1, v=1 with x=1, v=1.001). The motion of the ball may be seen as a symbol for more complicated dynamics.

Download plain Vga-PC Executable

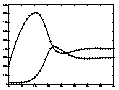LogoSimulation of student migration

This model (Scheurle/Seydel 1999) models the dynamics of numbers of students over a time period of 40 semesters. The dynamics varies with the number of freshmen. In the model, one group of students studies a special field (red curve), all other students are represented by the yellow curve. (The program is written in FORTRAN.)

Download plain Vga-PC Executable